In this article, we will teach you how to convert binary to decimal? Binary to decimal conversion is done by converting a given number in the binary number system to its equivalent value in the decimal number system. A number system is a format for representing numbers in a certain way. The binary number system is used in computers and electronic systems to represent data and consists of only two digits which are 0 and 1. Decimal number system is the most widely used number system in the world which can be easily understood by the people. It consists of digits from 0 to 9. Binary to decimal conversion can be performed in the simplest way by adding the products of each binary digit to it.
What is binary to decimal convert?
Binary to decimal conversion is done to help large binary numbers be easily read in a form that humans can understand. Every number system has a base and the base of a number system is determined by the total number of digits used in it.
For example, the base of the binary number system is 2 because it has only two digits to represent. Similarly, the base of the decimal number system is 10, as it takes 10 digits to represent a number. The binary number system that uses only two digits 0 and 1 is the most familiar number system for decimal numbers in general. Its base is 10 with only 10 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Convert binary to decimal formula:
The decimal number is equal to the sum of binary digits (dn) times their power of 2 (2n):
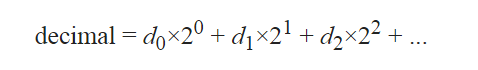
Methods of conversion from binary to decimal number system:
Here we have mainly described two methods to convert a binary number to a decimal number which are given below:
- Positional Notation Method
- Doubling Method
1 : Positional Notation Method
Using this method, write down the powers of two from right to left. Start at 20, evaluating it as “1“. Increment the exponent by one for each power. Stop when the amount of elements in the list is equal to the amount of digits in the binary number.
Example:
- The example of number 10011011, has eight digits, so the list, with eight elements, would look like this: 128, 64, 32, 16, 8, 4, 2, 1
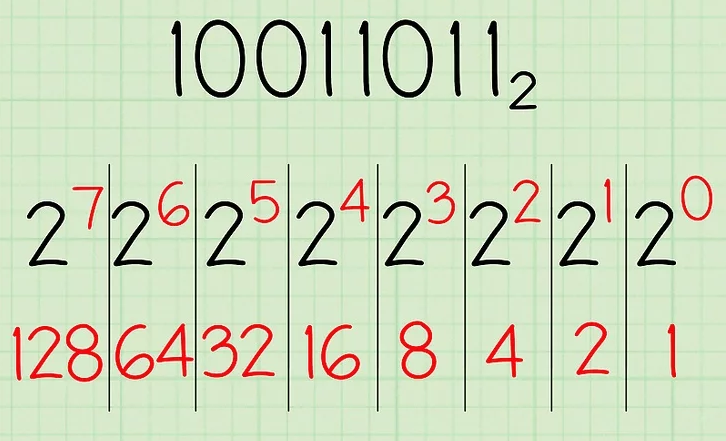
- Add up the numbers written below the line. Here’s what you do: 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 155. This is the decimal equivalent of the binary number 10011011.

- Finally, write the answer along with its base subscript look like: 15510
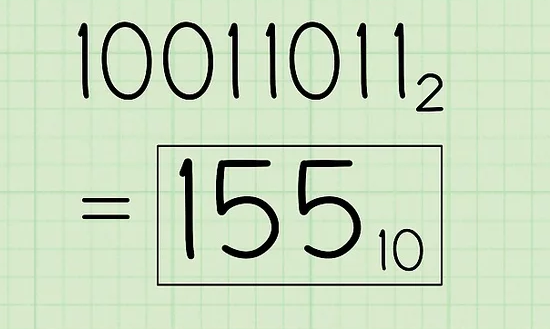
2 : Doubling Method
Using this method does not use up the powers. To convert binary integer to decimal, the leftmost digit has to be started by adding 0.
Example:
- Let’s say the number you are working with is 10110012. Write it as given in the image.
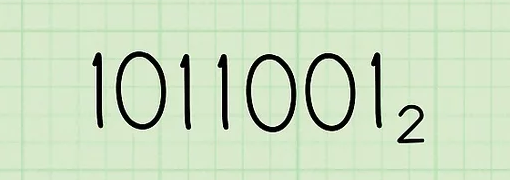
- Start by adding the left-most digit is 1, Next, multiply this by 2, and add the next digit in your number (as you progress from left to right) to this product.
- Since you are working with the binary number 10110012, your first digit on the left is 1. Your previous total is 0 because you haven’t started yet. You must double the previous total, add 0, and 1 to the current digit. 0 x 2 + 1 = 1, so your new current sum is 1.
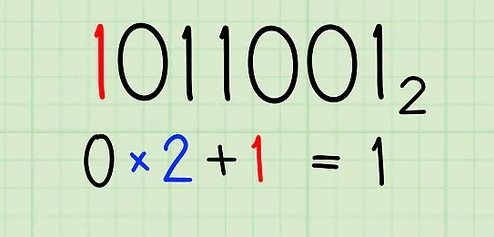
- Double your current total and add the next leftmost digit. Your current total is now 1 and the new current digit is 0. So, double 1 and add 0. to do that: 1 x 2 + 0 = 2. Your new current total is 2.
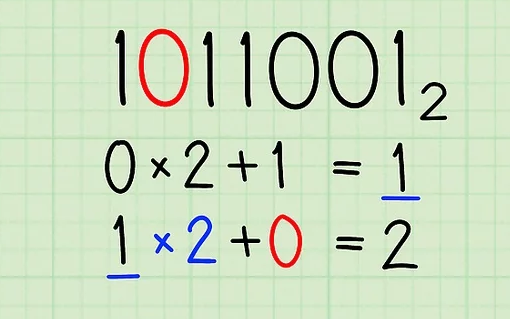
- Just keep going. Next, double your current total, and add 1, your next digit. 2 x 2 + 1 = 5. Your current total is now 5.
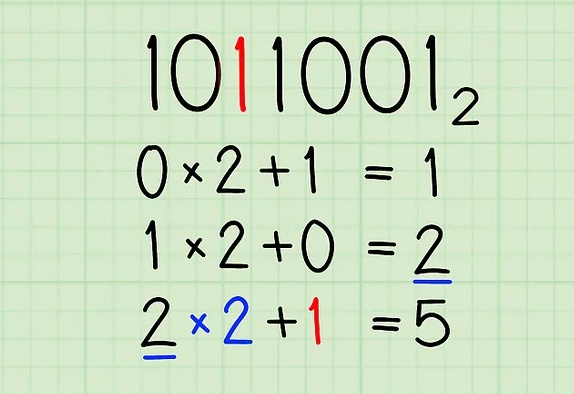
- Continue repeat the previous step.
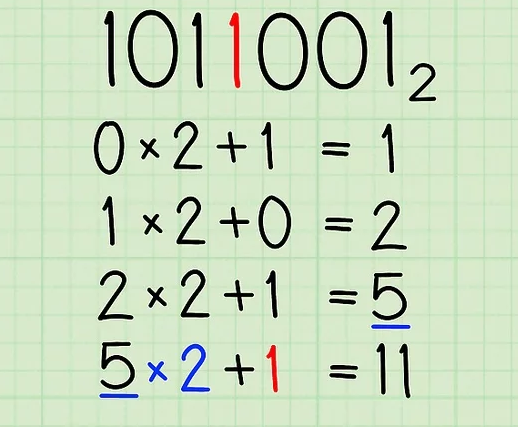
- Repeat the previous step again and again until you’ve run out of digits.
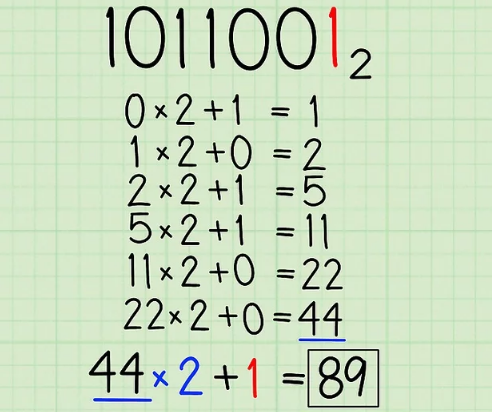
- You’re all done! You’ve converted 10110012 to decimal notation to its decimal form, 89.
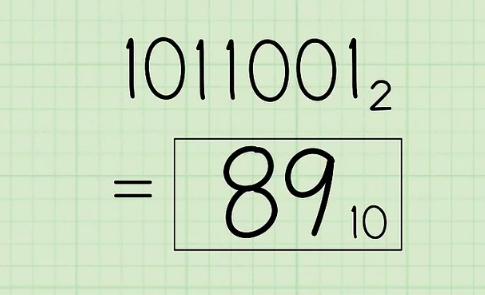
That’s all on how to binary to decimal? when you convert your binary number to decimal then read above methods. Here, we have provided two methods that you can try out. hope thsi is helpful to you.
