The square root of a number is the inverse operation of the square root of a number. The square of a number is the value obtained by multiplying a number by itself, whereas the square root of a number is the factorization of the number that is multiplied by itself to give the original number. If ‘a‘ is the square root of ‘b’, it means that a × a = b. The square of any number is always a positive number, so every number has two square roots, one for a positive value and one for a negative value. For example, 2 and -2 are both square roots of 4. However, in most places, only positive values are written as the square root of a number. Follow the steps given below to find the square root of a number.
How to find square roots in excel?
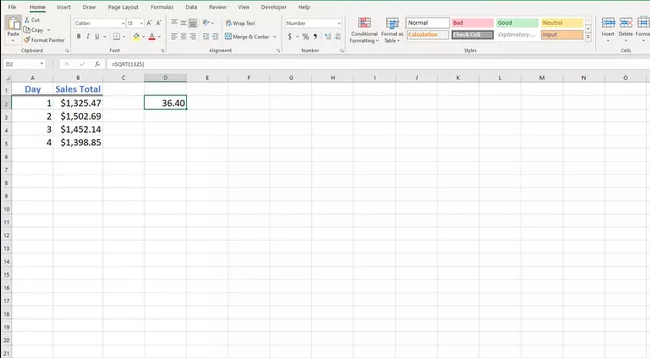
- Calculate a square root. The syntax for the SQRT() function is :
=SQRT(number)
To this function, you only need to pass the number argument, which is the number for which a square root needs to be found. This can be any positive number or cell reference to the location of the data in the worksheet.
- Compute an nth root. Use the POWER() function to calculate any original value :
=POWER(number,(1/n))
For the POWER() function, you will supply both the number and its exponent as arguments. To calculate a root, simply supply an inverse exponent—for example, a square root is 1/2.
The power() function is useful for both powers and exponents. for example :
=POWER(4,2)
yields 16, whereas :
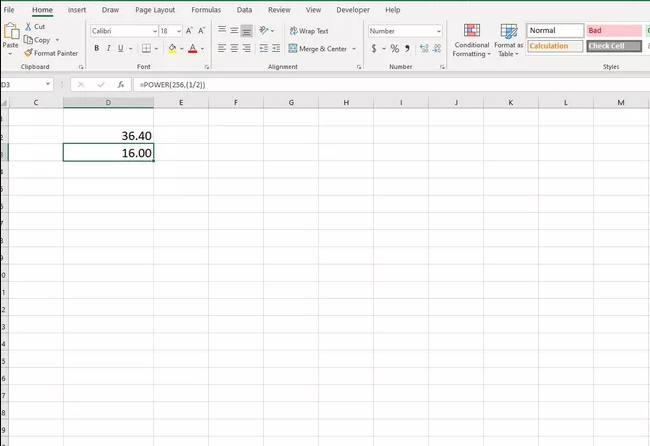
=POWER(256,(1/2))
Yields 16, which is the square root of 256. Roots are the inverse of powers.
Related: copy and paste square root
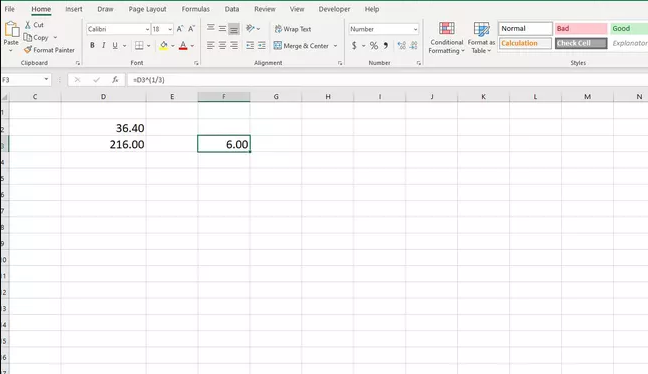
- Find Cube Root in Excel. To calculate the cube root of a number in Excel, use the caret operator (^) in a simple formula with 1/3 as the exponent.
=number^(1/3)
In this example, the formula =D3^(1/3) is used to find the cube root of 216, which is 6.
- Find the roots of imaginary numbers. Excel provides IMSQRT() and EMPOWER() functions to return the roots and powers of imaginary numbers. The syntax of these functions is the same as the real-number versions.